About

Postdoctoral Research Fellow, Applied PDE Group, AMCS, CEMSE, KAUST

\(\int_\Omega W(\nabla y_h) \rightarrow \int_\Omega W(\nabla y), \text{ as } h\rightarrow 0\)
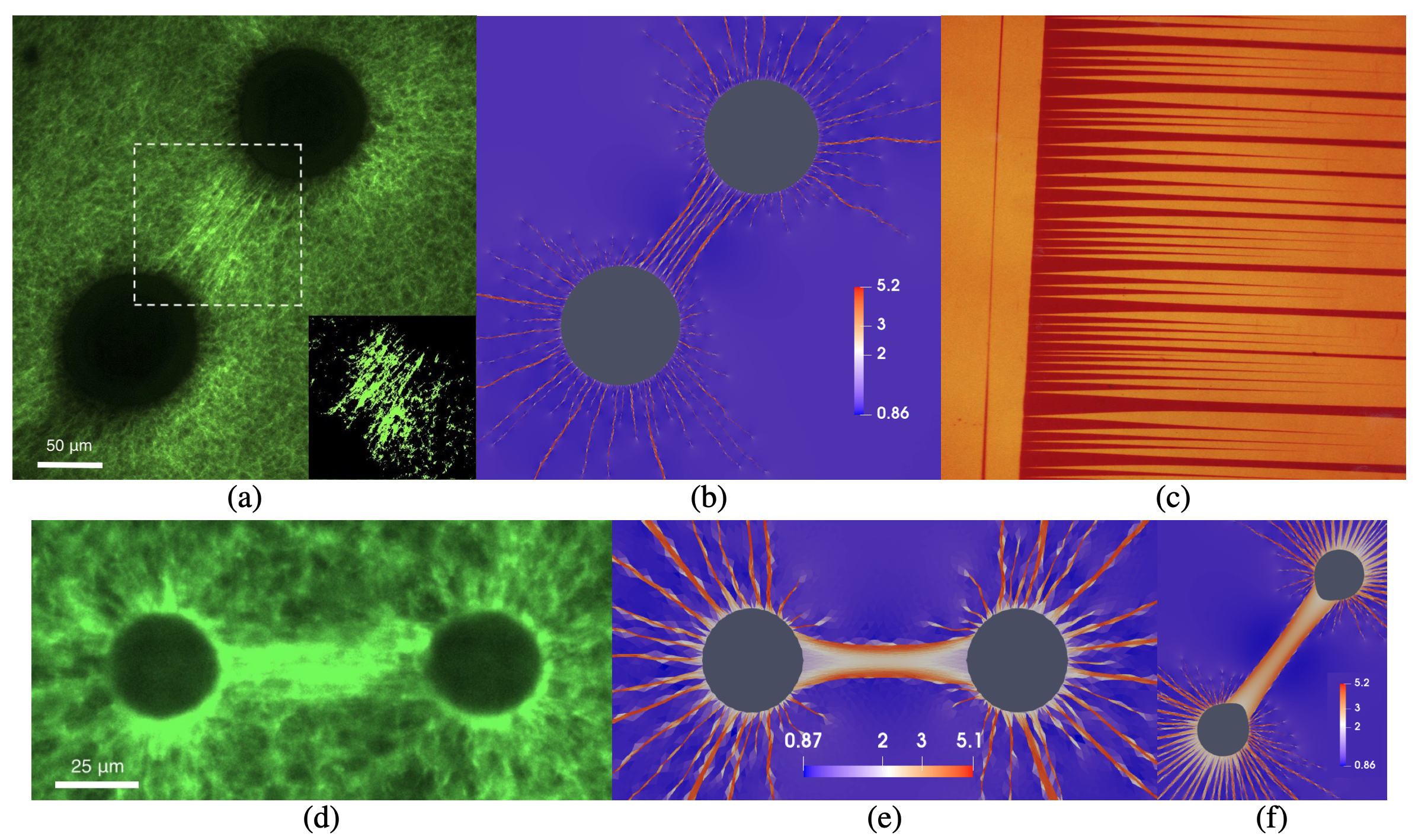
In the geometrically nonlinear theory of elasticity it is well known that under specific boundary conditions minimizing sequences arise, forming finer and finer microstructures in order to satisfy continuous deformations with discontinuous deformation gradients, where the deformation gradients belong to the energy wells. To understand better the behavior of the discrete minimization process we construct a two well (modulo rotations) elastic energy. Mimicking the austenite-martensite transitions, more precisely cubic to orthorhombic transformation, we choose the lattice parameters such that perfect interfaces are formed for the normals n=(1,0), n=(0,1), in the sense that continuous deformations with discontinuous deformation gradients at the energy wells are allowed along these normals.
Figure below: Discrete minimizers where red, blue colors indicate the attained phases orthorhombic, cubic respectively. The elastic energy is zero everywhere except the transition layers (green colors). Finer microstructures emerge for finer mesh resolution. Essentially the discrete minimizers capture elements of a sequence \(\{ y_k\} \in W^{1,\infty}(\Omega)\) such that such that \( y_k\stackrel{\ast}{\rightharpoonup} y_0\) in \(W^{1, \infty}(\Omega) \) where \(\{ \nabla y_k\} \) generates the unique homogeneous Young measure \(\nu_x = 0.5 \delta_I + 0.5 \delta_V\). We show that \(y_0\) is the minimiser of the relaxed problem. See https://doi.org/10.48550/arXiv.2501.11944.
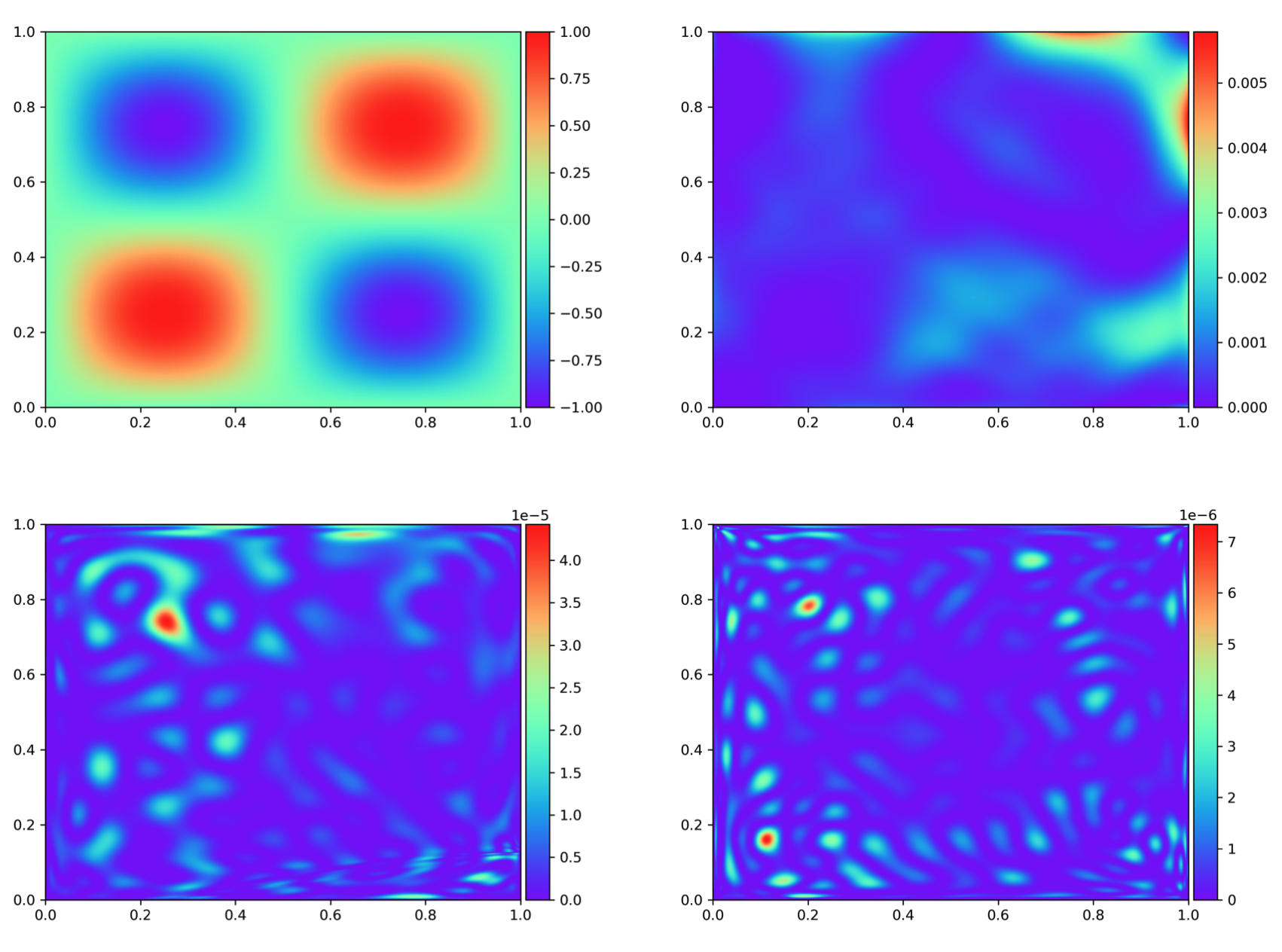
Approximating the solution of an energy (Deep Ritz method) where the exact solution is shown in the figure below, the point-wise square error is plotted for training through Monte-Carlo collocation (top right), quadrature collocation (bottom left) and training through finite elements (bottom right). The \( L^2(\Omega)\) error (not shown here) has been reduced by an order of magnitude for the proposed method, while the speed-up was in the range of 4-5 faster than the conventional training procedure for the given architecture. See https://doi.org/10.1016/j.cma.2025.117798.
Potassium sodium niobate is considered a prominent material system as a substitute for lead-containing ferroelectric materials. Potential applications range from energy conversion to innovative cooling technologies, thereby addressing important societal challenges. Recently Pop-Ghe et al. [2021 Ceramics International 47.14] synthesized Potassium Sodium Niobate (KNN) samples incorporating an excess of alkali metals during fabrication, suppressing inhomogeneous grain size distribution resulting in a significant fatigue behavior enhancement. For the fatigue optimized material she and her colleagues observed an unexplained phenomenon during the orthorhombic to tetragonal transition that they termed intermediate twinning.
To understand the appearance of intermediate twinning in this complex phase transformation we design a geometrically nonlinear electroelastic energy depending on the deformation gradient, spontaneous polarization and temperature. Evaluating explicitly the structure of the energy wells from X-ray diffraction measurements, we predict the observed transformations, intermediate twinning and detailed polarization as minimizers of the proposed free energy.
We show that phase transformations and spontaneous polarization in KNN are driven through compatibility conditions that ensure continuous deformations with discontinuous deformation gradients and pole-free interfaces, presenting a remarkable agreement between theory and experiment. The predictions are transferrable: the theory of geometrically nonlinear electrostriction given in our study provides a route to improve the reversibility of complex ferroelectric ceramics.
This study reveals that even if deformations are very small the response of the material is highly nonlinear. The model predicts the cubic to tetragonal transformation as a twinned laminate between the tetragonal variants (blue-green colors) which is compatible to the cubic phase (red color) in top left figure. Furthermore, the theoretical computed interfaces (top right image) forming a crossing twin are compared with the experimental observed orthorhombic phase (bottom left). It is remarkable that superimposing the two images (top right with bottom left) the theoretical interfaces coincide with the experimental observation. See https://doi.org/10.1007/s40830-025-00526-z.
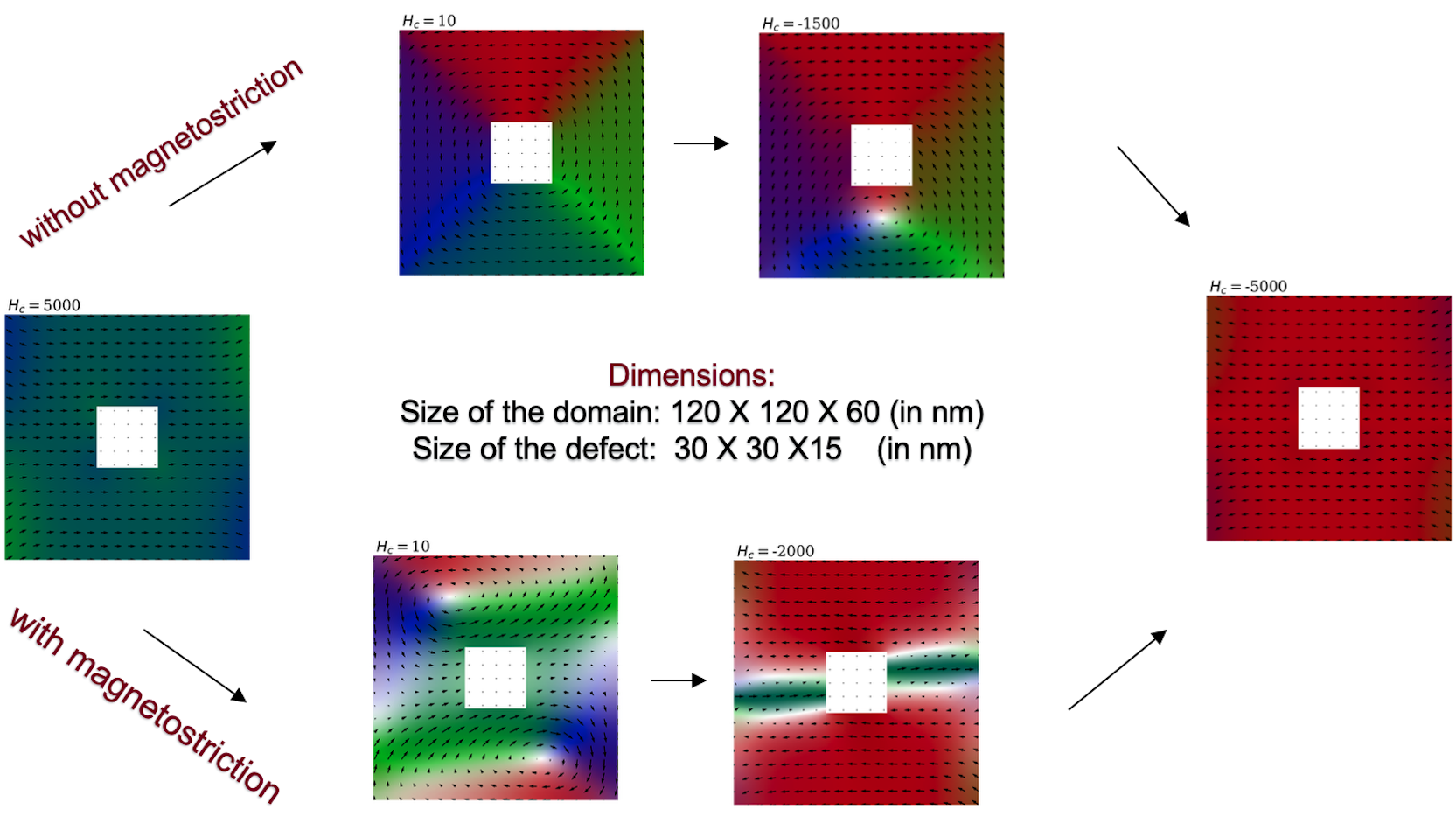
Image below: Magnetization on the plane z=0 for a 3-dimensional material with a defect (white enclosed region). Colors correspond to different angles on the xy plane.
Video below: A preliminary results for the discrete model. Here every edge of a square represents a fiber with a given constitutive law (linear response is shown). Viscous forces are neglected.